
Trigonometrija oko nas
U srijedu, 9.10.2019. smo malo pričekali da se raziđu oblici pa smo oko škole išli provjeriti da li možemo znanje trigonometrije primijeniti na neke jednostavne stvari oko nas. U glavnim ulogama su uskoro vrsni majstori instalateri-monteri iz 3.G razreda.
Od pribora smo ponijeli bilježnice i olovke, kutomjer i metar. Kutomjer smo malo preradili tako da kroz slamčicu lakše „nanišanimo“ objekt koji nam nije na dohvat ruke.
S kutomjerom rade dva učenika, jedan cilja objekt, a drugi pazi da je drugi krak položen vodoravno kako bismo dobili što točnije očitanje.
 |
 |
Kako je jutro bilo prilično prohladno, očitali smo samo mjeru kuta od zamišljene vodoravne linije od oka promatrača do vrha stupa ograde školskog igrališta i do vrha stupa rasvjete. Pri tom smo zabilježili i s koje udaljenosti smo radili očitanja.

U učionici smo na temelju mjerenja izračunali visinu stupa ograde i visinu stupa rasvjete. Evo kako smo to učinili za ogradu:
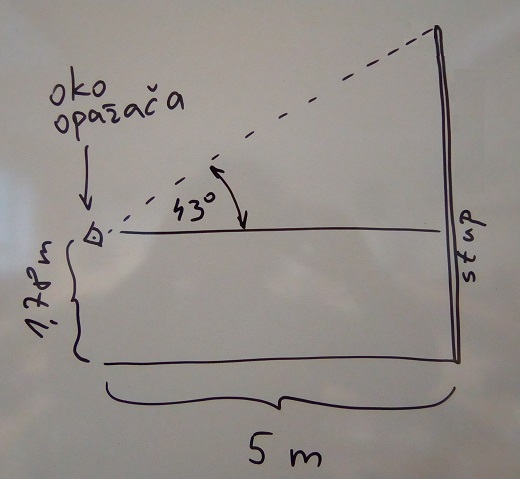 |
Prvo smo skicirali situaciju. Opažač je bio udaljen 5 m od ograde, a mjera kuta od zamišljene vodoravne crte od njegova oka do vrha stupa je 43°. |
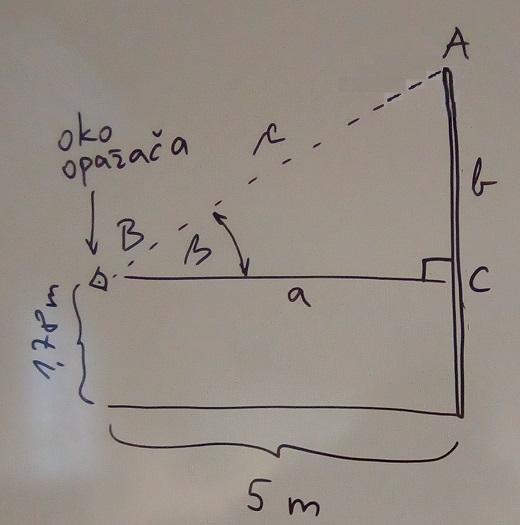 |
Zatim smo na skici uočili pravokutni trokut i obilježili vrhove A - vrh stupa, B - oko promatrača i C - točka u kojoj zamišljena vodoravna crta od oka promatrača dodiruje stup ograde. Nastavno tomu obilježili smo stranice trokuta i zaključili da znamo duljinu stranice a i mjeru kuta ß. |
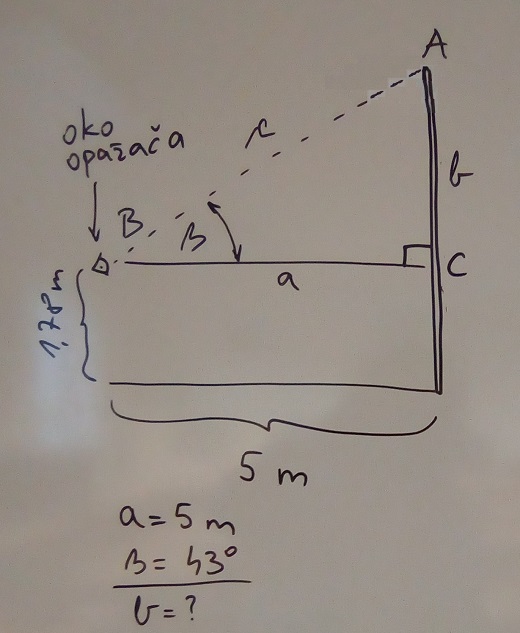 |
Da bismo izračunali visinu stupa ograde oko igrališta trebamo prvo izračunati duljinu stranice b kojoj ćemo onda dodati visinu od poda do opažačeva oka. |
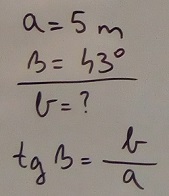 |
Kako znamo mjeru kuta i duljinu priležeće katete upotrijebit ćemo funkciju tangens. |
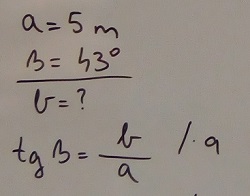 |
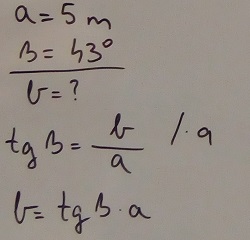 Da bismo se riješili razlomka i dobili nepoznatu duljinu stranice b na lijevoj strani izraza, cijeli izraz smo pomnožili s a. Da bismo se riješili razlomka i dobili nepoznatu duljinu stranice b na lijevoj strani izraza, cijeli izraz smo pomnožili s a. |
U izraz uvrstimo poznate vrijednosti i izračunamo stranicu b:
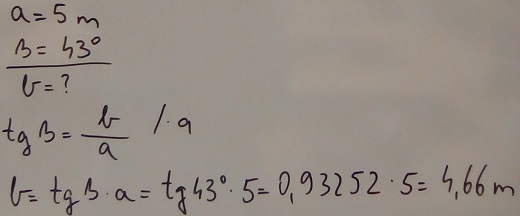 Tomu još treba dodati visinu od poda do oka učenika-opažača koja je u našem primjeru iznosila 178 cm i s obzirom na približnu točnost mjerenja kuta dobijemo i približnu visinu stupa:
Tomu još treba dodati visinu od poda do oka učenika-opažača koja je u našem primjeru iznosila 178 cm i s obzirom na približnu točnost mjerenja kuta dobijemo i približnu visinu stupa:
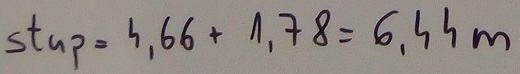
Visinu vratnice rukometnog gola i duljinu njene sjene iskoristili smo da izračunamo pod kojim kutom u tom trenutku sunčeve zrake padaju na igralište. Prvo smo mjerili i zabilježili.
 |
 |
Vratnica je visoka 2,08 m, a sjena je bila duga 5,79 m. To smo skicirali:
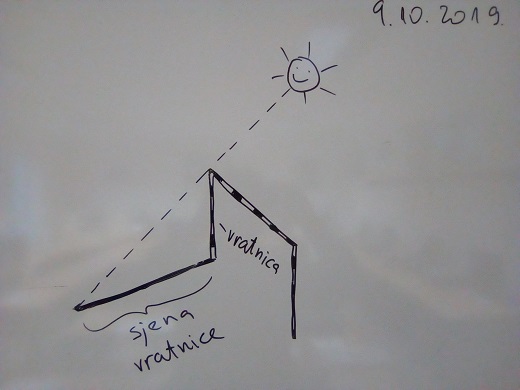 Zatim smo uočili pravokutni trokut i označili vrhove, stranice i kut.
Zatim smo uočili pravokutni trokut i označili vrhove, stranice i kut.
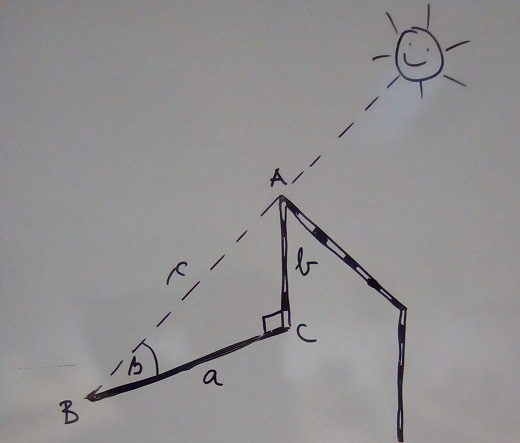 Zatim smo zapisali poznate veličine i ostaje nam izračunati mjeru kuta ß da bismo znali pod kojim kutom su sunčeve zrake padale na igralište.
Zatim smo zapisali poznate veličine i ostaje nam izračunati mjeru kuta ß da bismo znali pod kojim kutom su sunčeve zrake padale na igralište.
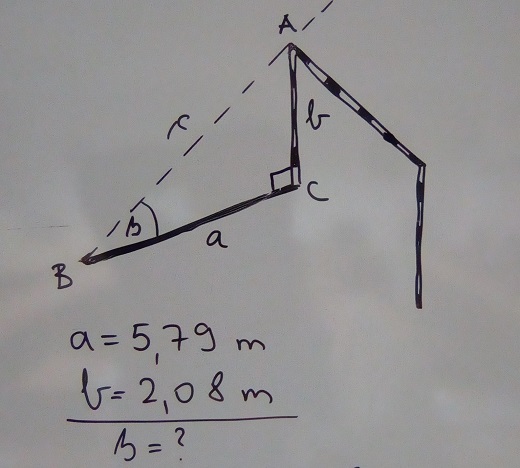
Kako znamo duljinu stranica a i b opet nam je prikladna funkcija tangens te smo u izraz uvrstili poznate veličine:
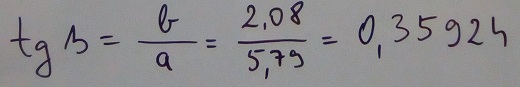
Dobivena vrijednost je tangens kuta ß, a nama treba mjera kuta ß. Stoga ćemo upotrijebiti inverznu funkciju tangensu, a to je arkus tangens. Na kalkulatoru moramo potražiti 2ndF ili INV i od našeg tangensa dobiti ćemo mjeru kuta:
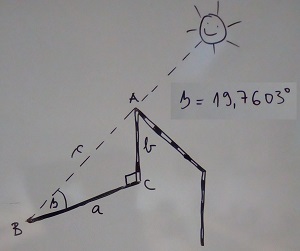 Naša mjerenja i izračun kažu da nas je 9. listopada 2019. godine u 9:02 sati u Križevcima Sunce vrlo slabo grijalo pod kutom od 19,7603°.
Naša mjerenja i izračun kažu da nas je 9. listopada 2019. godine u 9:02 sati u Križevcima Sunce vrlo slabo grijalo pod kutom od 19,7603°.
Prikažite to u stupnjevima, minutama i sekundama ![]() .
.
| « Travanj 2024 » | ||||||
| Po | Ut | Sr | Če | Pe | Su | Ne |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Učite s nama |  |
Državna matura |  |
Zanimljivosti |  |
Nadležne ustanove |  |

